MIPA Persamaan Kuadrat
MIPA Persamaan Kuadrat-MIPA Persamaan Kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah
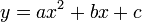
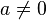
2. x1 - x2 = {(-b + √D) / 2a} - {(-b - √D) / 2a}
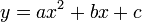
dengan
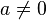
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari  , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
 , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
Cara menyelesaikan persamaan kuadrat ada 3, yaitu :
1. Memfaktorkan => (x-a) (x-b) = 0
Contoh :
a. X2 + 12x +32 = 0 => (x + 4) ( x + 8)
b. X2 + x – 56 = 0 => (x + 8) (x – 7)
c. X2 -6x – 27 = 0 => (x – 9) (x + 3)
d. 2x2 – 5x – 3 = 0 => (2x – 1) (x + 3)
e. 3x2 – 6x = 0 => 3x(x – 2)
2. Melengkapi Kuadrat Sempurna => (x - p)2 = q
Ada beberapa langkah, yaitu :
1. Koefisien x2 harus 1
2. Konstanta pindah ke ruas kanan {-> x2 + mx = n
3. Diubah ke bentuk kuadrat sempurna (x + p)2 = q
Contoh :
a. x2 + 8x + 12 = 0
x2 + 8x = -12
x2 + 8x + (1/2 . 8)2 = -12 + (1/2 . 8)2
x2 + 8x + 16 = -12 + 16
(x + 4)2 = 4
x + 4 = ±√4
x = -4 ± 2
x = -6 , -2
3. RUMUS ABC => x1,2 = { -b ± √(b2 - 4ac) } / 2a
Contoh :
a. x2 + 8x + 5 => x1,2 = { -8 ± √(82 – 4.1.5) } / 2.1
= { -8 ± √(64 – 20) } / 2
= ( -8 ± √39 ) / 2
Penjumlahan dan Pekalian akar2 Penyelesaian Persamaan Kuadrat
dari x1,2 = { -b ± √(b2 - 4ac) } / 2a dengan D = b2 - 4ac maka x1 = (-b + √D) / 2adan x2 = (-b - √D) / 2a
* D adalah Deskriminan
Penjumlahan dan Pekalian akar2 Penyelesaian Persamaan Kuadrat
dari x1,2 = { -b ± √(b2 - 4ac) } / 2a dengan D = b2 - 4ac maka x1 = (-b + √D) / 2adan x2 = (-b - √D) / 2a
* D adalah Deskriminan
1. x1 + x2 = {(-b + √D) / 2a} + {(-b - √D) / 2a}
= (-b + √D - b - √D) / 2a
= -2b / 2a
= -b /a
Jadi, x1 + x2 = -b/a
Jadi, x1 + x2 = -b/a
2. x1 - x2 = {(-b + √D) / 2a} - {(-b - √D) / 2a}
= (-b + √D + b + √D) / 2a
= 2√D / 2a
= √D /a
Jadi, x1 - x2 = √D/a
3. x1 . x2 = {(-b + √D) / 2a} {(-b - √D) / 2a}
= (b2 - D) / 4a2
= b2 - (b2 - 4ac) / 4a2
= (b2 - b2 + 4ac) / 4a2
= 4ac / 4a2
= c/a
Jadi, x1 . x2 = c/a
4. (x1 + x2)2 = x12 + 2(x1 . x2) + x22
(x1 + x2)2 - 2(x1 . x2) = x12 + x22
Jadi, x12 + x22 = (x1 + x2)2 - 2(x1 . x2)
5. (x1 + x2)3 = x13+ 3x12. x2 + 3x1 . x22 + x23
(x1 + x2)3 - 3x12. x2 + 3x1 . x22 = x13 + x23
(x1 + x2)3 - 3x1.x2(x1 + x2) = x13 + x23
Jadi, x13 + x23 = (x1 + x2)3 - 3x1.x2(x1 + x2)
4. (x1 + x2)2 = x12 + 2(x1 . x2) + x22
(x1 + x2)2 - 2(x1 . x2) = x12 + x22
Jadi, x12 + x22 = (x1 + x2)2 - 2(x1 . x2)
5. (x1 + x2)3 = x13+ 3x12. x2 + 3x1 . x22 + x23
(x1 + x2)3 - 3x12. x2 + 3x1 . x22 = x13 + x23
(x1 + x2)3 - 3x1.x2(x1 + x2) = x13 + x23
Jadi, x13 + x23 = (x1 + x2)3 - 3x1.x2(x1 + x2)
contoh soal!
1. Persamaan kuadrat -2x2 +4x-5=0 akar2nya α dan β
Tentukan : a. α + β d. α3 + β3
b. α . β e. 1/α + 1/β
c. α2 + β2 f. 1/(α+2) + 1/(β+2)
Jawaban :
a. α + β = -b/a = 2
b. α . β = c/a = 5/2
c. α2 + β2 = (α + β)2 - 2(α . β)
= 22 - 2.5/2
= 4 - 5
= -1
d. α3 + β3 = (α + β)3 - 3α.β (α+β )
= 23 - 3.5/2.2
= 8 - 15
= -7
e. 1/α + 1/β = (α + β) / αβ
= 2 / (5/2)
= 4/5
f. 1/(α+2) + 1/(β+2) = {(α+2) + (β+2)} / {(α+2) (β+2)}
= {(α+β) + 4} / {α.β + 2(α+β) + 4}
= (2+4) / (5/2 + 2.2 + 4)
= 6 / (21/2)
= 12/21
= 4/7
Menyusun Persamaan Kuadrat Baru
Ada 2 cara untuk menyusun persamaan kuadrat baru yang akar2nya x1 dan x2 yaitu,
1. (x - x1) (x - x2) = 0
Contoh soal : Susunlah Persamaan kuadrat baru yang akar2nya adalah
a. 2 dan 7 => PKB = (x - 2) (x -7)
= x2 - 9x +14
b. -3 dan -4 => PKB = {x-(-3)} {x-(-4)}
= (x+3) (x+4)
= x2 + 7x + 12
c. -7 dan 2 => PKB = {x-(-7)} (x-2)
= (x+7) (x-2)
= x2 + 5x - 14
d. 5 dan -2 => PKB = (x-5) {x-(-2)}
= (x-5) (x+2)
= x2 - 3x - 10
2. x2 - (x1 + x2)x + x1.x2 = 0
Contoh soal :
1. Susunlah Persamaan Kuadrat baru yang akar2nya adalah 2+√5 dan 2-√5!
Jawaban : x1 + x2 = (2+√5) +(2-√5) = 4
x1.x2 = (2+√5) (2-√5) = -1
Jadi, PKB => x2 - (x1 + x2)x + x1.x2 = 0
=> x2 - 4x - 1 = 0
2. x1 dan x2 adalah akar2 persamaan kuadrat x2 - 2x + 5 = 0. Susunlah persamaan kuadrat baru yang akar2nya3 lebihnya dari akar2 persamaan kuadrat yang diletahui.
Jawaban : x1 + x2 = -b/a = 2 dan x1.x2 = c/a = 5
x1 = (x1 + 3) dan x2 = (x2 + 3)
maka, x1 + x2 = (x1 + 3) + (x2 + 3) dan x1.x2 = (x1 + 3) (x2 + 3)
= (x1 + x2) + 6 = x1.x2 + 3(x1+x2) + 9
= 2 + 6 = 5 + 3.2 + 9
= 8 = 20
Jadi, PKB => x2 - (x1 + x2)x + x1.x2 = 0
=> x2 - 8x + 20 = 0
* Deskriminan (D) => D = b2 - 4ac *
untuk menentukan jenis akar2 persamaan kuadrat, rumusnya :
a. D = 0 => Mempunyai 2 akar yang sama
b. D < 0 => Tidak mempunyai akar nyata (akar2nya imajiner)
c. D ≥ 0 => Mempunyai 2 akar nyata
d . D > 0 => Mempunyai 2 akar nyata dan berlawanan
Contoh Soal :
1. Tentukan nilai k agar persamaan kuadrat kx2 + 3x + k = 0 mempunyai 2 akar sama/kembar
Jawaban : Syarat akar kembar D = 0, maka
b2 - 4ac = 32 - 4.k.k
0 = 9 - 4k2
4k2 = 9
k = √(9/4)
k = ± 3/2
2. Tentukan m agar persamaan kuadrat berikut x2 - 2x + (m+1) = 0 Tidak mempunyai akar nyata.
Jawaban : Syarat tidak mempunyai akar nyata D < 0, maka
b2 - 4ac < 0
22 - 4.1.(m+1) < 0
4 - 4m - 4 < 0
0 - 4m < 0
- 4m < 0
m > 0
3. Tentukan P agar persamaan kuadrat x2 + px + p = 0 mempunyai 2 akar real dan berbeda.
Jawaban : Syarat akar real dan berbeda D > 0, maka
b2 - 4ac > 0
p2 - 4.1.p > 0
p2 - 4p > 0
p(p - 4) > 0
Jadi, p < 0 dan p > 4


Comments
Post a Comment